By Martin Medeiros
Readers of my blog should know of the decision support criteria that game theory offers. I use it to determine outcomes of deal negotiations, mediation, arbitration and litigation. Thinking I would have some fun with the model, and with clothespin on my nose watching U.S. politics in particular, I offer a text book analysis on what to do if you are associated with one party and want to “defect” or leave your party’s policy decision. We will assume that at least two functioning parties are good for the democratic tradition of our republic. We use trade policy as our example.
We all know the odds of one “party” winning and you may recall the eponymous “Prisoner’s Dilemma” in economics or negotiation class, but let’s look into the decision criteria one party could use as they are in a real crisis.
We know most Americans fall into the broad “moderate” category, but we like to define parties and construct differences, which do exist. Consistency is valued and generally that is the equilibrium of our policy. In the short-term, hypocrisy and contradiction captivate attention, generally, and in the media specifically. The man bites the dog interests us. Free trade is boring.
Are trade policies now crazy or crazy like a fox? Game theory has great and, perhaps, decisive predictor of influence on guiding the outcome of the negotiation or dispute in many situations. Game theory attempts to mathematically analyze behavior in strategic situations in which an individual’s success in making choices depends on the choices of others and reactions to those choices. A study of this dynamic should be considered a tool in the long-term section of a negotiators toolbox, but its actual use may be tactical, or a in a particular short-term activity (as explained later). The word “strategic” is used here because much of this analysis is done, if at all, prior to the negotiation. It is this analysis that is of high importance to understand the systems approach supported by my approach to my practice generally, and negotiations specifically. How does knowledge of game theory impact the individual actor, whether a single person or nation?
Politicians correctly may identify themselves as a “people person” and enjoy the softer sciences of human interaction. They may eschew math and other stereotypically introverted pursuits. These negotiators are at a competitive disadvantage unless they understand the core of game theory. Ultimately, we seek to find “rational” behavior based on personalities involved, outcomes, probabilities of those outcomes and payoffs. Richard Thaler informs us that “rational” behavior can be preselected through an exercise called “choice architecture.” But given enough trials, even homo sapiens irrational behavior can reach a predictable equilibrium.
The “game” in game theory is a metaphor for human interactions in economics or politics. Knowing that game theory is a practical or applied field of mathematics that deals with outcomes between agents, parties representing interests of themselves or others. Much like the fields populated by trade negotiators, diplomats, politicians or attorneys, there is more in the negotiation system than just positions.
Game theory extends basic optimization theory of the neo-classical economists—remember the guns and butter exercises? These focused on supply and demand, costs, outputs, and revenue distribution, optimization of utility and profits, and peoples’ tendency to act differently on complete knowledge—by adding the sociological variables of opposing agents. We may then change our positions based on others’ actions: I will put up a 25% tariff on apples because you put up a 20% tariff on olives. For example of how this works, if my actions may change based on the response of another, game theory is perfect for negotiation analysis. In neoclassical economics, one “wins” when one settles on a price perceived as mutually beneficial or when one takes the lion’s share from a competitor based not on what a competitor does, but what is filtered through the market data of supply and demand. If one is influenced by a competitor in a price competition or auction, game theory comes into play. Von Neumann and Morgenstern pioneered this theory in 1944[1] and outlined so-called “forms.” These forms can help us understand outcomes in a negotiation.
Think of the old mercantilist zero sum game, a Pareto dynamic. If you are “winning” or if I do not feel like I am winning, I must be losing. This theory gave way to theories of comparative and competitive advantages: growing sugar from beets or corn in Montana is less effective than producing sugar from Sugar Cane in Brazil.
Resolutions happen whether or not humans at the polls, the electoral college, or automated agents (such as the banking Automated Clearing House “ACH” technology we use every day but never see in banking) and the new Smart Contracts using blockchain, are part of the system to interfere with natural outcomes of a negotiation system. Simply put, the singular act of individual negotiator injecting himself or herself into the system changes the outcome, all things being equal. And this election cycle of 2016 had some pretty anomalous injections that present us with the current trade policy. Recall, to set up our analysis we will need to know the potential outcomes, the probability and the payoff. We will put the personalities aside for now.
Before getting into the “game of game theory”, negotiators need to know what their options are. But consider the simple example of a three-element trade deal, I like to see it as a public negotiation. The outcome formula may be represented by:
C=RI
C=number of possible outcomes
R=number of resolutions
I=issues to be negotiated.
For example, if there are 2 resolutions (accept or reject) and 3 issues (tariffs, tax cuts and transfer payments) to negotiate there are 23 or 8 possible outcomes (e.g., policy).
Applying this to a policy where there are our three issues: tariffs (taxes on imports), tax cuts (for domestic businesses) and transfer payments (price supports), we can tabulate the outcomes to allow our thoughts to coalesce. Two possible resolutions: (1) accepted or agreeable (indicated as a “+”) and (2) unaccepted or disagreeable (indicated as a “-“). In our example we can place this in tabular form:
| Solution | Tariff | Tax | Transfer |
| 1 | + | + | + |
| 2 | + | + | – |
| 3 | + | – | + |
| 4 | + | – | – |
| 5 | – | + | + |
| 6 | – | + | – |
| 7 | – | – | + |
| 8 | – | – | – |
If we decide that tax and tariff are “non-negotiable”, there are only two outcomes to negotiate with, Solution 1 and Solution 2. The rest can be eliminated immediately. Even if your party gets to this stage, the negotiation is easier because the universe of options is limited. Now that we have options, we can go further into game theory “what if” planning.
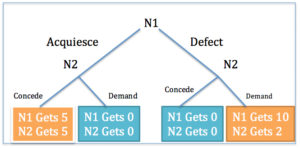
Applied to the international negotiation dynamic, the extensive form of expressing game theory is a diagrammatic representation of the popular “decision tree,”—where nodes are decision points—and includes a number of elements: (1) the number of negotiators in a transaction, (2) the options, resolutions, or outcomes for the negotiator, (3) the knowledge of each negotiator at every move and, (4) the payoffs of the negotiator at various combination of moves. Below is the extensive form diagram with N1 being, for example, a politician wishing to negotiate to deescalate tensions, and N2 being a politician wishing to defect from the party wanting to deescalate. The options are to support or negotiate (leaving aside the fact that a defection can be a negotiation tactic). Each negotiator can concede or demand. For our exercise, the payoffs here are assigned values (10, 5, 2, or 0), which should represent the “money” at stake (bully pulpit notwithstanding, taxes fund policy). The payoff could be anything that is being negotiated: increase in tariffs, decrease taxes, increase state intervention in transfers, increase or decrease in taxes variable to be negotiated in the legislature. This is different than a risk/reward analysis because N1’s choice will influence N2’s action.
The normal form of expressing game theory is the basic matrix, but the same elements must be expressed. So in our simplified union strike example:
| Party | N2 | ||
| Decision | Chooses to Negotiate | Chooses to Defect | |
| N1 | Chooses Demand | 0, 0 | 10, 2 |
| Chooses Concede | 5, 5 | 0, 0 | |
Table 1.2: Game Theory: Normal Form
This form is used in the seminal prisoner’s dilemma game.
In the classroom of psychologists at Stanford University[2], mathematician A. W. Tucker described one of the most basic applications of game theory. This is the classic matrix used in the so-called “prisoner’s dilemma,” or “PD” here, where one caught conspirator can confess to a crime and testify against to the other.[3] The prisoner confessing the crime goes free if the other is convicted. So the choices are cooperating with the criminal enterprise or “defect” or leaving the criminal conspiracy enterprise and “ratting out” your colleague in crime. If no conspirator talks, both get a reduced sentence. If they both confess, each will get more than the reduced sentence, but not as long of a sentence as the convicted prisoner would if one “rats” and the other is convicted. Rational behavior dictates both will confess because there is the possibility of going free or getting less time, but the confessor does not know what the other conspirator is deciding to do. The PD issue is that they are kept in separate rooms so there is no information exchange.
In the normal form we would see the duration of incarceration for the prisoners’ move. In the free trade dynamic, this construct may work for bilateral, but not multilateral. The game theory model is much more complex. As Dartmouth researchers informed us last year, when tariff negotiations are constrained to satisfy the most favored nation rule and multilateral reciprocity, trade is conducted at a fixed world price – but this model assumed three nations in a two good transaction. That is not what we have today. A supported premise is that multilateral free trade agreements are the best solution generally. But specifically, a globally-sustainable-Pareto-optimal bilateral deal is possible for only very special cases according to researches Demet Yilmazkudayy and Hakan Yilmazkuday. You may recal that Pareto optimal is tainted with the zero sum game rubric, this denotes a distribution of wealth such that any redistribution or other change beneficial to one individual is detrimental to one or more others (if one entity pays taxes, I may support another via a transfer (price support) that was triggered by the tariff.
An example is what we may call the “Iterated Prisoner’s Dilemma,” which has a potentially infinite number plays. This helps us to find the Nash equilibrium, where will a trade war, or the parties settle at. Each player has an opportunity to retaliate against the other player for previous non-cooperative negotiation. Cooperation may then arise as an equilibrium outcome. The benefits of cooperation may outweigh the pain of punishment, leading to the Nash Equilibrium. For example, in the PD, defection is the Nash Equilibrium.
| Prisoner 2 | |||
| Action | Confess | Remain Silent | |
| Prisoner 1 | Confess | 10 years, 10 years | 0 years, 20 years |
| Remain Silent | 20 years, 0 years | 1 year, 1 year | |
If they both confess, they each get ten years. If prisoner 1 remains silent, and prisoner 2 confesses, Prisoner 1 gets twenty years and prisoner 2 goes free. If they both remain silent, they both are charged with the lesser offense and get one year. One prisoner can reason, “it is always better to confess because it is worse to get 20 years if the other confesses and I stay silent. But if I confess, either he may get twenty or I will share a ten-year sentence. To avoid the maximum, it makes sense to confess with a chance of going free.” Alternatively, if both prisoners remain silent, they get the lesser offense, but one risks being ratted out. So “rational” behavior, leads one to confess, but there may be an irrational actor. So how to we classify the dominant strategy?
The dominant strategy applied to a negotiation emerges when a negotiator in a game separately evaluates the options, based on his choice and the other negotiator’s choice. So rational behavior dictates that the negotiator looks for the best payoff; in the PD, what would give him the less time? Remaining silent will never yield the shortest sentence, 0 years, but confession will. So, without information being passed, the dual confession is called a “dominant equilibrium” and it yields a suboptimal situation in the PD with both prisoners getting 10 years. In fact, each party is worse off than their individual self-interest because the response of the other party alters their outcome. Rational behavior by one prisoner yields a smaller payoff. But this academic exercise yields assumes what the rational action is, that there is no communication, that there is no mistrial where the parties are back in court making potentially different decisions. The situation the United States fins itself involves a series of bad subjective decisions, and will continue to do so if this extends to policy-making on subjective rather than objective data (e.g., climate change, not knowing the definition of a scientific theory, eschewing free trade, thinking voters can focus on 12 candidates debating at once for multiple sessions, etc.). The PD model may not fit many situations. It has been examined in the litigation context,[4] but may not fit with multi-party disputes. What, then, does the negotiator need in order to focus the disputants on an issue? Does this manufactured focal point beyond the relative payoff have utility? Can it be used against a negotiator’s interest?
The Issue With World Trade in the 21st Century
Even though centuries of data support the fallacy in mercantilism and the flaws of effectively managing many bilateral trade talks; politicians favor these ideas. Parties are irrelevant, the party of liberalization in trade today, will be the party of protectionism tomorrow; the party of capitalism will turn socialist if it means concentration of power. How do we then, nudge people into looking at objective data?
Multilateral trade is a Thalerian “nudge” to get individuals to act rationally, but not always optimally. Bilateralism allows nations to sweat the little stuff, and given enough time, effort and presence. The analysis above assumes bilateral parties and bilateral choices: concede or defect. Multiparty negotiations yield certain behaviors unlike our simple two-party construct. Indications are that bilateral will not help the post-Brexit UK. It seems unlikely to help the post NAFTA, post WTO America. There are simply too many variables.
The words of John Nash are timeless:
In general terms, we idealize the bargaining problem by assuming that the two individuals are highly rational, that each can accurately compare his desires for various things, that they are equal in bargaining skill, and that each has full knowledge of tastes and preferences of the other.[11]
I am certain none of these conditions are observed presently.
[1] Morgenstern, Oskar, and John Von Neumann. Theory of Games and Economic Behavior. Princeton University Press, 1980.
[2] Hagenmayer, S. J. Obituary: “Albert W. Tucker, 89, Famed Mathematician,” The Philadelphia Inquirer. Feb. 2, 1995.
[3] Davis, Morton. Game theory a nontechnical introduction. New York: Basic Books, 1983. p. 108
[4]Gilson, Ronald J., and Robert H. Mnookin. “Disputing through Agents: Cooperation and Conflict between Lawyers in Litigation.” Columbia Law Review 94.2 (1994): 509-566.
[5] Schelling, Thomas C. The strategy of conflict. Harvard University Press, 1980.
[6] Ibid.
[7] Schelling, T.C. Micromotives and macrobehavior. WW Norton & Company, 2006.
[8] It is widely reported that many more Democrats subscribe to scientific social media feeds than Republicans do.
[9] Davis, Morton. Game theory a nontechnical introduction. New York: Basic Books, 1983. p. 122
[10] Myerson, Roger. Game theory : analysis of conflict. Cambridge, Mass.: Harvard University Press, 1991. p. 97
[11] Nash, John F. “The Bargaining Problem.” Econometrica 18.2 (1950): 155-162.